Next: 第22章 Windows Up: 応用理工学情報処理 Previous: 第20章 C 言語 II Contents Index
#include <stdio.h>
#include <stdlib.h>
/*
1から100までの和を求め, 画面(標準出力)に出力するプログラム.
keyword: for
*/
int main(void)
{
int i;
int sum=0;
for(i=1; i<=100; i++)
sum += i;
printf("sum=%d\n", sum);
return EXIT_SUCCESS;
}
#include <stdio.h>
#include <stdlib.h>
/*
n! を求め, 標準出力に出力する.
keywords: for
*/
int main(void)
{
int i, factorial, n;
n = 4;
factorial = 1;
for(i=1; i<=n; i++)
factorial *= i;
printf("The factorial of %d is %d.\n", n, factorial);
return EXIT_SUCCESS;
}
#include <stdio.h>
#include <stdlib.h>
/*
関数 f(x)= x^2 を 0から1まで積分した値を近似的に求める.
解析解は1/3.
keywords: for
*/
int main(void)
{
int i;
double x0=0.0, x1=1.0;
int n = 10;
double h = (x1-x0)/n;
double x;
double integral = 0.0;
x=x0;
for(i=0; i<n; i++){
integral += x*x * h;
x += h;
}
printf("n=%d, h=%g, integral=%g\n", n, h, integral);
return EXIT_SUCCESS;
}
#include <stdio.h>
#include <stdlib.h>
/*
関数 f(x)= x^2 を 0から1まで積分した値を求める.
解析解は1/3.
区間をn分割し, 積分値をI_{n}を求める. 分割数nを増やし,
I_{n} - I_{n-1}が与えられた値 tolerance より小さくなったとき,
収束したこととする.
keywords: do while
*/
int main(void)
{
int i;
double h; /* 分割した各領域の幅*/
double x0=0.0, x1=1.0; /* 積分区間 */
int n; /* 分割数 */
double x; /* 積分変数 */
double integral = 0.0; /* = I_{n} */
double integral_previous = 0.0; /* = I_{n-1}*/
double error; /* = |I_{n} - I_{n-1}|. 差.*/
double tolerance = 1.0e-8; /* error < tolerance になったら終了*/
n = 9;
do{
n++;
integral_previous = integral;
h = (x1-x0)/n;
x=x0;
integral = 0.0;
for(i=0; i<n; i++){
integral += x*x * h;
x += h;
}
if(integral>=integral_previous)
error = integral - integral_previous;
else
error = integral_previous - integral;
printf("n=%d, h=%g, integral=%g, with an error of %g\n",
n, h, integral, error);
}while(error>tolerance);
return EXIT_SUCCESS;
}
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
/*
関数 f(x)= x^2 を 0から1まで積分した値を求める.
解析解は1/3.
被積分関数を関数として独立させた.
*/
/* 被積分 */
double f(double x)
{
return x*x;
}
int main(void)
{
int i;
double h; /* 分割した各領域の幅*/
double x0=0.0, x1=1.0; /* 積分区間 */
int n; /* 分割数 */
double x; /* 積分変数 */
double integral = 0.0; /* = I_{n} */
double integral_previous = 0.0; /* = I_{n-1}*/
double error; /* = |I_{n} - I_{n-1}|. 誤差.*/
double tolerance = 1.0e-8; /* error < tolerance になったら終了*/
n = 9;
do{
n++;
integral_previous = integral;
h = (x1-x0)/n;
x=x0;
integral = 0.0;
for(i=0; i<n; i++){
integral += f(x) * h;
x += h;
}
error = fabs(integral - integral_previous);
printf("n=%d, h=%g, integral=%g, with an error of %g\n",
n, h, integral, error);
}while(error>tolerance);
return EXIT_SUCCESS;
}
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
/*
関数 f(x)= x^2 を 0から1まで積分した値を求める.
被積分関数fと積分を行う関数integralを関数として独立させた.
*/
/* 被積分 */
double f(double x)
{
return x*x;
}
double integral(int n, double x0, double x1)
{
int i;
double h = (x1-x0)/n; /* 分割した各領域の幅*/
double x=x0; /* 積分変数 */
double val = 0.0;
for(i=0; i<n; i++){
val += f(x) * h;
x += h;
}
}
int main(void)
{
double x0=0.0, x1=1.0; /* 積分区間 */
int n; /* 分割数 */
double integral = 0.0; /* = I_{n} */
double integral_previous = 0.0; /* = I_{n-1}*/
double error; /* = |I_{n} - I_{n-1}|. 誤差.*/
double tolerance = 1.0e-8; /* error < tolerance になったら終了*/
n = 9;
do{
n++;
integral_previous = integral;
integral_current = integral(n, x0, x1);
error = fabs(integral - integral_previous);
printf("n=%d, h=%g, integral=%g, with an error of %g\n",
n, h, integral, error);
}while(error>tolerance);
return EXIT_SUCCESS;
}
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
/*
関数 f(x)= x^2 を 0から1まで積分した値を求める.
解析解は1/3.
被積分関数を関数として独立させた.
その積分する関数に, 被積分関数を与えられるようにした.
keyword: 関数へのポインタ
*/
/* ---------------------------------------------------------------- */
double integral(int n, double x0, double x1, double (*fn)(double x))
{
int i;
double h = (x1-x0)/n; /* 分割した各領域の幅*/
double x=x0; /* 積分変数 */
double val = 0.0;
for(i=0; i<n; i++){
val += fn(x) * h;
x += h;
}
return val;
}
/* ----------------------------------------------------------------- */
/* 被積分 */
double f(double x)
{
return x*x;
}
int main(void)
{
double x0=0.0, x1=1.0; /* 積分区間 */
int n; /* 分割数 */
double integral_current = 0.0; /* = I_{n} */
double integral_previous = 0.0; /* = I_{n-1}*/
double error; /* = |I_{n} - I_{n-1}|. 誤差.*/
double tolerance = 1.0e-8; /* error < tolerance になったら終了*/
n = 9;
do{
n++;
integral_previous = integral_current;
integral_current = integral(n, x0, x1, f);
error = fabs(integral_current - integral_previous);
printf("n=%d, integral=%g, with an error of %g\n",
n, integral_current, error);
}while(error>tolerance);
return EXIT_SUCCESS;
}
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
/*
関数 f(x)= x^2 を 0から1まで積分した値を求める.
積分を行う関数, 積分値が収束するまで分割数を増やす関数を関数として独立させた.
do_integral では, do ... while を用いた例を示すために, do ... while を
用いている. 関数によっては do ... while のループを脱出できず,
無限ループになる可能性がある. 従って, n が大きくなりすぎたら
do ... while のループを脱出(break)するようにしておく必要がある.
しかし, その場合には do ... while を用いるよりも for を用いた方が
よいであろう.
*/
double integral(int n, double x0, double x1, double (*fn)(double x))
{
int i;
double h = (x1-x0)/n; /* 分割した各領域の幅*/
double x=x0; /* 積分変数 */
double val = 0.0;
for(i=0; i<n; i++){
val += fn(x) * h;
x += h;
}
return val;
}
double do_intgral(double (*fn)(double x), double x0, double x1,
double tolerance)
{
int n; /* 分割数 */
double integral_current = 0.0; /* = I_{n} */
double integral_previous = 0.0; /* = I_{n-1}*/
double error; /* = |I_{n} - I_{n-1}|. 誤差.*/
n = 9;
do{
n++;
integral_previous = integral_current;
integral_current = integral(n, x0, x1, fn);
error = fabs(integral_current - integral_previous);
printf("n=%d, integral=%g, with an error of %g\n",
n, integral_current, error);
}while(error>tolerance);
return integral_current;
}
/*
-----------------------------------------------------------------
以降を変更するだけで積分が求められるようになる.
-----------------------------------------------------------------
*/
/* 被積分 */
double f(double x)
{
return x*x;
}
int main(void)
{
double x0=0.0, x1=1.0; /* 積分区間 */
double tolerance = 1.0e-8; /* 精度 */
do_intgral(f, x0, x1, tolerance);
return EXIT_SUCCESS;
}
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
/*
三角関数sin(x) をマクローリン展開により近似して求める.
sin x = x - x^3/3! + x^5/5! - ...
= Σ_{i=1}^n ( sign * power / factorial )
*/
int main(void)
{
int i, j;
long factorial; /* = i! */
double power; /* = x^i*/
double sign = -1.0; /* 加えるときの符号 */
double x = 0.1; /* 求めようとする x の値. */
int n = 11; /* 次数 */
double sum = 0.0; /* 計算結果を保持. */
for(i=1; i<=n; i+=2){
sign *= -1.0;
/* iの階乗 i! を求める. */
factorial = 1;
for(j=1; j<=i; j++)
factorial *= j;
printf("The factorial of %d is %ld.\n", i, factorial);
/* xの冪乗 x^i を求める. */
power = 1.0;
for(j=0; j<i; j++)
power *= x;
printf("The %d-th power of %g is %g.\n", i, x, power);
sum += sign*power/factorial;
printf("%d: sin(%g) = %g with an error of %g\n\n",
i, x, sum, sum-sin(x));
}
return EXIT_SUCCESS;
}
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
/*
三角関数sin(x) をマクローリン展開により近似して求める.
sin x = x - x^3/3! + x^5/5! - ...
= Σ _{i=1} ^n ( sign * power / factorial )
iの階乗 i! を求める関数 factorial と
xの冪乗 x^i を求める関数 power を関数として独立させた.
keyword: 関数
*/
/* iの階乗 i! を求める. */
double factorial(int i)
{
int j;
double f = 1.0;
for(j=1; j<=i; j++)
f *= (double)j;
printf("The factorial of %d is %g.\n", i, f);
return f;
}
/* xの冪乗 x^i を求める. */
double power(double x, int i)
{
int j;
double p = 1.0;
for(j=0; j<i; j++)
p *= x;
printf("The %d-th power of %g is %g.\n", i, x, p);
return p;
}
int main(void)
{
int i;
double sign = -1.0; /* 加えるときの符号 */
double x = 0.1; /* 求めようとする x の値. */
int n = 11; /* 次数 */
double sum = 0.0; /* 計算結果を保持. */
for(i=1; i<=n; i+=2){
sign *= -1.0;
sum += sign * power(x, i) / factorial(i);
printf("%d: sin(%g) = %g with an error of %g\n\n",
i, x, sum, sum-sin(x));
}
return EXIT_SUCCESS;
}
M_PI がπの値として定義されている場合がある。
この場合は 例えば次のようにしてその値を用いることができる。
#include <stdio.h>
int main(void)
{
double pi;
pi = M_PI;
printf("pi = %g\n", x);
return 0;
}
atan を使う.
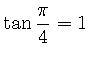 すなわち
すなわち
![]() の
関係を利用できる.
の
関係を利用できる.
#include <stdio.h>
#include <math.h>
int main(void)
{
double pi;
pi = 4.0 * atan(1.0);
printf("pi = %g\n", pi);
return 0;
}
/*
=== ネピアの定数 ===
lim (1 + 1/n) ^n = e をネピアの定数という. (e = 2.71828...)
n→∞
以下では数値的にこの値を求める.
*/
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
int main(void)
{
long int i, n;
double a, e;
for (n=1; n<20; n++) {
a = 1.0 + 1.0/(double)n;
e = 1.0;
for (i = 0; i < n; i++){
e *= a;
}
printf("[%ld] e = %g\n", n, e);
}
return 0;
}
/*
プログラムが正しいかどうかは 以下のようにして検算できる.
printf("[1] e = %g\n", (1.0+1.0/1.0));
printf("[2] e = %g\n", (1.0+1.0/2.0)*(1.0+1.0/2.0));
printf("[3] e = %g\n", (1.0+1.0/3.0)*(1.0+1.0/3.0)*(1.0+1.0/3.0));
*/
#include <stdio.h>
#include <stdlib.h>
/*
* 二進数で表示する関数.
* verbose <= 10 の時: 2 進数で表示する.
* verbose >10 の時: 更に, 桁数を表す数字とマーカーを表示する.
*/
void print_2_shin(char *msg, unsigned x, int verbose)
{
char str[ 8*sizeof(x) + 1 ];
char *ptr;
int i;
ptr = str + sizeof(str) -1;
*ptr-- = '\0';
for( ; ptr>=str; x>>=1)
*ptr-- = x&1 ? '1' : '0';
ptr++;
if(verbose>10){
printf(msg);
for(i=0; i<sizeof(x); i++)
printf("76543210");
printf("\n");
printf("%s", msg);
for(i=0; i<sizeof(x); i++)
printf("-------+");
printf("\n");
}
printf("%s%s\n", msg, ptr);
}
int main(void)
{
unsigned x = 10u;
unsigned y = 15u;
print_2_shin(" x =", x, 0);
print_2_shin(" y =", y, 0);
print_2_shin(" ~x =", ~x, 0); /* 1 の補数 (ビットの反転) */
print_2_shin("x<<1 =", x << 1, 0); /* 1 ビット右にシフト */
print_2_shin("x<<2 =", x << 2, 0); /* 2 ビット右にシフト */
print_2_shin("x>>3 =", x >> 3, 0); /* 3 ビット左にシフト */
print_2_shin(" x|y =", x | y, 0); /* OR */
print_2_shin(" x&y =", x & y, 0); /* AND */
print_2_shin(" x^y =", x ^ y, 0); /* exclusive OR */
return 0;
}
こういうのもいいかも知れない.
#include <stdio.h>
char *reverse(char *str)
{
int i, j;
char c;
for(i=0, j=strlen(str)-1; i<j; i++, j--){
c = str[i];
str[i] = str[j];
str[j] = c;
}
return str;
}
char *print_2_shin(int x)
{
int i = 0;
static char str[8*sizeof(x) + 1];
do {
str[i++] = x&1 ? '1' : '0';
} while( x>>=1 );
return reverse(str);
}
int main(void)
{
int x = 15;
printf("%d = %s\n", x, print_2_shin(x));
return 0;
}
#include <stdio.h>
int main(void)
{
int i;
for(i=32; i<128; i++)
printf("%d (0x%x) '%c'\n", i, i, i);
return 0;
}
#include <stdio.h>
FILE *my_fopen(const char *filename, const char *mode)
{
FILE *ptr = fopen(filename, mode);
if(ptr == NULL){
perror(filename);
exit(1);
}
return ptr;
}
int main(void)
{
FILE *fp;
fp = my_fopen("data.dat", "w");
fprintf(fp, "aaa\n");
fprintf(fp, "bbb\n");
fclose(fp);
return 0;
}
#include <stdio.h>
#include <stdlib.h>
void *my_malloc(size_t size)
{
void *ptr;
ptr = (void *)malloc(size);
if(ptr == NULL){
perror("memory allocation error");
exit(1);
}
return ptr;
}
int main(void)
{
int i, n;
double *x, *y;
n = 10;
x = (double *)my_malloc( n * sizeof(double) );
y = (double *)my_malloc( n * sizeof(double) );
for(i=0; i<n; i++){
x[i] = i;
y[i] = 10.0 * i;
}
for(i=0; i<n; i++)
printf("%g, %g\n", x[i], y[i]);
free(x);
free(y);
return 0;
}
#include <stdio.h>
#include <stdlib.h>
/*
rand関数は stdlib.h で
int rand(void);
とプロトタイプ宣言されている. #include <stdlib.h> が必要.
rand関数は, [0, RAND_MAX] の範囲の整数値を返す疑似乱数関数である.
ここで, RNAD_MAX は stdlib.h で与えられている定数で,
環境により適切に設定されている.
*/
int main(void)
{
unsigned int x;
x = rand();
printf("RAND_MAX = %u\n", RAND_MAX);
printf("rand = %u\n", x);
return 0;
}
rand 関数を何度か呼び出してみると, 何回実行しても同じ整数が同じ順序で得られる. プログラムを作成する最中は, 毎回異なる値になると再現性がなくむしろ困るかもしれない.
#include <stdio.h>
#include <stdlib.h>
/*
rand関数は stdlib.h で
int rand(void);
とプロトタイプ宣言されている. #include <stdlib.h> が必要.
rand関数は, [0, RAND_MAX] の範囲の整数値を返す疑似乱数関数である.
ここで, RNAD_MAX は stdlib.h で与えられている定数で,
環境により適切に設定されている.
*/
int main(void)
{
int i;
unsigned int x;
printf("RAND_MAX = %u\n", RAND_MAX);
for(i=0; i<10; i++){
x = rand();
printf("rand = %u\n", x);
}
return 0;
}
乱数は, ある値からいつも定まった操作で得られているで, 最初の値を変更すれば異なる乱数列が得られる. この値を設定するのがsrand関数である.
#include <stdio.h>
#include <stdlib.h>
/*
rand関数は stdlib.h で
int rand(void);
とプロトタイプ宣言されている. #include <stdlib.h> が必要.
rand関数は, [0, RAND_MAX] の範囲の整数値を返す疑似乱数関数である.
ここで, RNAD_MAX は stdlib.h で与えられている定数で,
環境により適切に設定されている.
rand関数は, seed (種) から順次擬似的にランダムな値を求めている.
seed は特に指定していない場合は 1 になっている. 指定する場合は,
stdlib.h で
void srand(unsigned int seed);
と宣言されているsrand関数を用いる.
これを用いることにより別の乱数列が得られる.
*/
int main(void)
{
int i;
unsigned int x;
unsigned int seed = 30; // seed を変更すれば別の乱数列が得られる.
srand(seed);
printf("RAND_MAX = %u\n", RAND_MAX);
for(i=0; i<10; i++){
x = rand();
printf("rand = %u\n", x);
}
return 0;
}
![]() の範囲の実数の乱数は次のようにして得られる.
の範囲の実数の乱数は次のようにして得られる.
#include <stdio.h>
#include <stdlib.h>
/*
#include <stdlib.h>
int rand(void);
void srand(unsigned int seed);
rand 関数は [0, RAND_MAX]の範囲のランダムな整数を返す.
*/
int main(void)
{
int i;
double x;
unsigned int seed = 30; // seed を変更すれば別の乱数列が得られる.
srand(seed);
for(i=0; i<10; i++){
x = (double)rand()/RAND_MAX; // x は [0.0, 1.0]の範囲の乱数.
printf("rand = %g\n", x);
}
return EXIT_SUCCESS;
}
乱数を用いて円の面積を求めてみる. これから円周率が得られる.
#include <stdio.h>
#include <stdlib.h>
/*
乱数を用いてπの値を求める.
(x, y) は, [0,1]X[0,1]の範囲の乱数とする.
x*x + y*y <= 1 のとき(x,y)は円の内側である.
第一象限の円の内側の面積 / [0,1]X[0,1]の面積
= (1/4 π*1*1) / 1*1 = π/4
である.
従って, (x,y)を[0,1]X[0,1]の範囲でランダムに発生させると,
(x,y)が円内である回数 / (x,y)を発生させた回数 = π/4となる.
これから, πの値を求める.
*/
int main(void)
{
unsigned int i, n_max = 10000, in=0;
double x, y;
unsigned int seed = 30; // seed を変更すれば別の乱数列が得られる.
srand(seed);
for(i=0; i<n_max; i++){
x = (double)rand()/RAND_MAX;
y = (double)rand()/RAND_MAX;
if(x*x + y*y <=1.0)
in++;
printf("%d: (x, y) = (%g, %g), %d\n", i, x, y, in);
}
printf("in/n_max*4 = %d/%d*4 = %g\n", in, n_max, 4.0*in/n_max);
return EXIT_SUCCESS;
}
精度を高くするために, unsigned long intを用いてみる. 各点の値を出力するprintfの部分は遅くなるので省略しておく.
#include <stdio.h>
#include <stdlib.h>
/*
乱数を用いてπの値を求める.
(x, y) は, [0,1]X[0,1]の範囲の乱数とする.
x*x + y*y <= 1 のとき(x,y)は円の内側である.
第一象限の円の内側の面積 / [0,1]X[0,1]の面積
= (1/4 π*1*1) / 1*1 = π/4
である.
従って, (x,y)を[0,1]X[0,1]の範囲でランダムに発生させると,
(x,y)が円内である回数 / (x,y)を発生させた回数 = π/4となる.
これから, πの値を求める.
*/
int main(void)
{
unsigned long int i, n_max = 1000000000, in=0;
double x, y;
unsigned int seed = 30; // seed を変更すれば別の乱数列が得られる.
srand(seed);
for(i=0; i<n_max; i++){
x = (double)rand()/RAND_MAX;
y = (double)rand()/RAND_MAX;
if(x*x + y*y <=1.0)
in++;
// printf("%d: (x, y) = (%g, %g), %d\n", i, x, y, in);
}
printf("in/n_max*4 = %ld/%ld*4 = %g\n", in, n_max, 4.0*in/n_max);
return EXIT_SUCCESS;
}
struct timeval tv1, tv2;
gettimeofday(&tv1, NULL);
c = read(fd, buf, data_size);
gettimeofday(&tv2, NULL);
calc = (1e6*(tv2.tv_sec - tv1.tv_sec)) + (tv2.tv_usec - tv1.tv_usec);
printf("\n%d samples / %lu usec = %f k samples/sec\n",
data_size/2, calc,
(float)(data_size/2)/((float)calc*1e-3));
#include <stdio.h>
#define N 4
double average(double *x, int n)
{
int i;
double sum = 0.0;
for(i=0; i<n; i++)
sum += x[i];
return sum/(double)n;
}
int main(void)
{
double a[N] = {1.0, 2.0, 3.0, 4.0};
double avr;
avr = average(a, N);
printf("average = %g\n", avr);
return 0;
}
平均値を求めるプログラム.
#include <stdio.h>
#include <stdlib.h>
/*
平均値を求めるプログラム.
配列の要素数は sizeof(a)/sizeof(a[0])で得られる.
keyword: sizeof
*/
double average(double *x, int n)
{
int i;
double sum = 0.0;
for(i=0; i<n; i++)
sum += x[i];
return sum/(double)n;
}
int main(void)
{
double a[] = {1.0, 2.0, 3.0, 4.0};
int n = sizeof(a)/sizeof(a[0]); // 要素数
double avr;
avr = average(a, n);
printf("average = %g\n", avr);
return EXIT_SUCCESS;
}
標準偏差を求める. ここで平方根を求める数学関数sqrtが必要となる. このような数学関数については [19.4.1]を参照のこと.
#include <stdio.h>
#include <math.h>
/*
分散を求めるプログラム.
sqrt は平方根を求める関数.
math.h でプロトタイプ宣言されているので, #include <math.h>とする必要がある.
gcc でコンパイルする時には libm の中に含まれる sqrt関数を用いることとする.
その場合, libm から lib を外した m を -lオプションを用いて指定する.
プログラムのファイル名を deviation.cとすると
$ cc deviation.c -lm
のようにファイル名の後ろに指定する.
*/
#define N 4
double average(double *x, int n)
{
int i;
double sum = 0.0;
for(i=0; i<n; i++)
sum += x[i];
return sum/(double)n;
}
double deviation(double *x, int n)
{
int i;
double avr = 0.0, sigma2 = 0.0, dev;
avr = average(x, n);
for(i=0; i<n; i++)
sigma2 += (x[i] - avr) * (x[i] - avr);
dev = sqrt(sigma2/n); // sqrt は平方根を求める関数.
// n-1で割る流儀もある.
return (dev);
}
int main(void)
{
double a[N] = {1.0, 2.0, 3.0, 4.0};
double dev;
dev = deviation(a, N);
printf("standard deviation = %g\n", dev);
return 0;
}
標準偏差を求める.
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
/*
分散を求めるプログラム.
sqrt は平方根を求める関数.
*/
double average(double *x, size_t n)
{
size_t i;
double sum = 0.0;
for(i=0; i<n; i++)
sum += x[i];
return sum/(double)n;
}
double deviation(double *x, size_t n)
{
int i;
double sigma2 = 0.0;
double avr = average(x, n);
for(i=0; i<n; i++)
sigma2 += (x[i] - avr) * (x[i] - avr);
return sqrt(sigma2/n);
}
int main(void)
{
double a[] = {1.0, 2.0, 3.0, 4.0};
int n = sizeof(a)/sizeof(a[0]);
printf("standard deviation = %g\n", deviation(a, n));
return EXIT_SUCCESS;
}
まずは ![]() 関数の値を出力するプログラムを作ってみる.
関数の値を出力するプログラムを作ってみる.
#include <stdio.h>
#include <math.h>
int main(void)
{
FILE *fp;
double x;
if( (fp=fopen("data.dat", "w")) == NULL )
exit(1);
for(x=0.0; x<10.0; x+=0.1)
fprintf(fp, "%g %g\n", x, sin(x));
fclose(fp);
return 0;
}
出力した結果は gnuplot [24.5.1] や Excel 等を使ってグラフ化でき
る.
もう少し, 一般性を高くしてみる.
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
int main(void)
{
FILE *fp;
char *filename;
double x, x0, x1, dx;
int samples;
double (*func)(double x);
/* ここで全ての設定をする. */
filename = "data.dat";
x0 = 0.0;
x1 = 10.0;
samples = 100;
dx = (x1-x0)/samples;
func = sin;
if( (fp=fopen(filename, "w")) == NULL ){
perror(filename);
exit(EXIT_FAILURE);
}
for(x=x0; x<x1; x+=dx)
fprintf(fp, "%g %g\n", x, (*func)(x));
fclose(fp);
return EXIT_SUCCESS;
}
関数化してみる.
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
int plot(char *filename,
double x0, double x1, int samples,
double (*func)(double x))
{
FILE *fp;
double x, dx;
if( (fp=fopen(filename, "w")) == NULL ){
perror(filename);
return 1;
}
dx = (x1-x0)/samples;
for(x=x0; x<x1; x+=dx)
fprintf(fp, "%g %g\n", x, (*func)(x));
fclose(fp);
return 0;
}
int main(void)
{
int ret;
ret = plot("data1.dat", 0.0, 10.0, 100, sin);
ret += plot("data2.dat", 0.0, 10.0, 100, cos);
return ret;
}
引数の順序や数を変えたくなることはよくあるが, 変えてしまうとその関数を 呼び出している全ての部分を変更する必要がある. 構造体を使うことでこの問 題を解決できる.
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
struct plotdata {
char *filename;
double x0;
double x1;
int samples;
double (*func)(double x);
};
int plot(struct plotdata dat)
{
FILE *fp;
double x, dx;
if( (fp=fopen(dat.filename, "w")) == NULL ){
perror(dat.filename);
return 1;
}
dx = (dat.x1 - dat.x0) / dat.samples;
for(x=dat.x0; x<dat.x1; x+=dx)
fprintf(fp, "%g %g\n", x, (*dat.func)(x));
fclose(fp);
return 0;
}
int main(void)
{
int ret1, ret2;
struct plotdata data;
data.filename = "data1.dat";
data.x0 = 0.0;
data.x1 = 10.0;
data.samples = 100;
data.func = sin;
ret1 = plot(data);
data.filename = "data2.dat";
data.func = cos;
ret2 = plot(data);
return ret1+ret2;
}
ここで示したように 1つの構造体の中にデータをまとめてしまうと, 同じ構造
を持つたくさんのデータを扱うのが容易になる. 又, 操作や演算を行なう関数
もこの構造体を受け取るようにしておくと見通しがよくなる. 例えば 次のよ
うに拡張していくことができる. 構造体のメンバーにに char *name; を加え,
![]() 関数を追加した.
関数を追加した.
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
struct plotdata {
char *filename;
double x0;
double x1;
int samples;
char *name;
double (*func)(double x);
};
int plot(struct plotdata dat)
{
FILE *fp;
double x, dx;
if( (fp=fopen(dat.filename, "w")) == NULL ){
perror(dat.filename);
return 1;
}
dx = (dat.x1 - dat.x0) / dat.samples;
for(x=dat.x0; x<dat.x1; x+=dx)
fprintf(fp, "%g %g\n", x, (*dat.func)(x));
fclose(fp);
return 0;
}
void report(struct plotdata dat)
{
printf("filename: %s\n", dat.filename);
printf("range: [%g, %g]\n", dat.x0, dat.x1);
printf("samples: %d\n", dat.samples);
printf("function: %s\n", dat.name);
}
int main(void)
{
int ret1, ret2;
struct plotdata data1, data2;
data1.filename = "data1.dat";
data1.x0 = 0.0;
data1.x1 = 10.0;
data1.samples = 100;
data1.name = "sin";
data1.func = sin;
data2.filename = "data2.dat";
data2.x0 = 0.0;
data2.x1 = 10.0;
data2.samples = 100;
data2.name = "cos";
data2.func = cos;
report(data1);
ret1 = plot(data1);
report(data2);
ret1 = plot(data2);
return ret1+ret2;
}
一行当りのデータを表現している文字数や, データの個数が不明なときには,
実行時に行を読み込むための領域やデータを保持する領域を増やしていけばい
い. これを行なうには malloc で確保した領域を realloc に
より 拡張していけばいい. 例えば次のようになる.
load_data 関数の中の static size_t num_max = 2;,
do_fgets 関数の中のstatic size_t buffer_len = 2;
と const size_t block_size = 2; は動作がよくわかるように非常に小
さな値にしてある. 実際には warning が出ない程度に大きくしておく方がい
い.
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
void *do_realloc(void *old, size_t size)
{
void *new;
new = realloc(old, size);
if(new == NULL){
perror("do_realloc: allocation error:");
exit(1);
}
return new;
}
FILE *do_fopen(char *format, char *mode)
{
FILE *fp = fopen(format, mode);
if(fp==NULL){
perror("do_fopen");
}
return fp;
}
/*
|<------buffer_len--------------------------->|
| |
| |<-- block_size -->|
| | |
+--------------------------+------------------+
| buffer | additional block |
+--------------------------+------------------+
| |
| |
buffer buffer + buffer_len - block_size
*/
char *do_fgets(FILE *fp)
{
static char *buffer = NULL;
static size_t buffer_len = 2;
size_t len;
const size_t block_size = 2;
int i;
const int i_max = 100;
char *ptr, *ret;
if( ! buffer )
buffer = do_realloc(NULL, buffer_len * sizeof(char));
ptr = buffer;
len = buffer_len;
for(i=0; i<i_max; i++){
ret = fgets(ptr, len, fp);
if( ret == NULL)
return NULL;
if( strchr(ptr, '\n') )
return buffer;
fprintf(stderr,
"warning: do_fgets:buffer reallocated. [%s]\n", buffer);
buffer_len += block_size;
buffer = do_realloc(buffer, buffer_len * sizeof(char));
ptr = buffer + buffer_len - block_size -1;
len = block_size+1;
}
fprintf(stderr, "faital error:do_fgets:\n");
return NULL;
}
size_t load_data(FILE *fp, double **x, double **y)
{
double tmp_x, tmp_y;
char *line;
static size_t num_max = 2;
size_t num;
/* 十分と予想される程度に大きな領域を確保しておく.*/
*x = do_realloc(NULL, num_max * sizeof(double));
*y = do_realloc(NULL, num_max * sizeof(double));
num = 0;
while( (line=do_fgets(fp)) != NULL ){
if( (sscanf(line, "%lf %lf", &tmp_x, &tmp_y) == 2)
|| (sscanf(line, "%lf, %lf", &tmp_x, &tmp_y) == 2) ){
(*x)[num] = tmp_x;
(*y)[num] = tmp_y;
num++;
} else {
fprintf(stderr, "Invalid:%s", line);
}
if(num>=num_max){
/*足りなくなったら, 領域を拡張する.*/
num_max *= 2;
*x = do_realloc(*x, num_max * sizeof(double));
*y = do_realloc(*y, num_max * sizeof(double));
fprintf(stderr,
"warning: load_data: data buffer is re-allocated.\n");
}
}
/* 読み込んだデータと丁度同じ領域を確保しそこに移動する. */
*x = do_realloc(*x, num * sizeof(double));
*y = do_realloc(*y, num * sizeof(double));
return num;
}
size_t do_load_data(char *filename, double **x, double **y)
{
size_t n;
FILE *fp;
fp = do_fopen(filename, "r");
if (fp==NULL)
return 0;
n = load_data(fp, x, y);
fclose(fp);
return n;
}
int main(void)
{
size_t i, n;
double *x, *y;
n = do_load_data("data.dat", &x, &y);
for(i=0; i<n; i++)
printf("(%g, %g)\n", x[i], y[i]);
free(x);
free(y);
return 0;
}
#include <stdio.h>
#include <stdlib.h>
/*
N次元のベクトル同士の和,差,内積を求める.
keyword: 配列
*/
#define N 5
int main(void)
{
int i;
double x;
double v1[N] = {1.0, 2.0, 3.0, 4.0, 5.0};
double v2[N] = {6.0, 7.0, 8.0, 9.0, 10.0};
double v3[N] = {0.0};
/* 和 */
for(i=0; i<N; i++)
v3[i] = v1[i] + v2[i];
/* 差 */
for(i=0; i<N; i++)
v3[i] = v1[i] - v2[i];
/* 内積 */
x=0.0;
for(i=0; i<N; i++)
x += v1[i]*v2[i];
for(i=0; i<N; i++)
printf("v3[%d]=%g\n", i, v3[i]);
printf("x=%g\n", x);
return EXIT_SUCCESS;
}
#include <stdio.h>
#include <stdlib.h>
/*
N次元のベクトル同士の和,差,内積を求める.
それぞれの演算を行うための関数を作成した.
keyword: 配列, define, マクロ, malloc
変更する可能性のある変数はできるだけ define された値をを使わない.
ここでは, 配列の宣言時のみ N を用いている.
多くの配列の大きさを変える簡便な方法として define を用いた.
本来は malloc を用いるべき.
*/
#define N 5
/* 和 */
void add(double v3[], double v1[], double v2[], int n)
{
int i;
for(i=0; i<n; i++)
v3[i] = v1[i] + v2[i];
/* 呼出側の配列の値が変更されることに注意. */
/* C言語では配列を返す関数がないので, */
/* このように呼出側で配列を用意してその内容を変更する. */
}
/* 差 */
void subtract(double v3[], double v1[], double v2[], int n)
{
int i;
for(i=0; i<n; i++)
v3[i] = v1[i] - v2[i];
}
/* 内積 */
double product(double v1[], double v2[], int n)
{
int i;
double x = 0.0;
for(i=0; i<n; i++)
x+= v1[i]*v2[i];
return x;
}
/* ベクトルの内容を表示. */
void print_vector(double v[], int n)
{
int i;
for(i=0; i<n; i++)
printf("v[%d]=%g\n", i, v[i]);
}
int main(void)
{
double x;
double v1[N] = {1.0, 2.0, 3.0, 4.0, 5.0};
double v2[N] = {6.0, 7.0, 8.0, 9.0, 10.0};
double v3[N] = {0.0};
add(v3, v1, v1, N);
subtract(v3, v1, v2, N);
x = product(v1, v2, N);
print_vector(v3, N);
printf("x=%g\n", x);
return EXIT_SUCCESS;
}
#include <stdio.h>
#include <stdlib.h>
/*
N次元のベクトル同士の和,差,内積を求める.
配列の宣言に可変長配列を用いた.
keyword: 配列, define, マクロ, C99
#define で定義されたマクロはできる限り用いない.
C99では,可変長配列を用いる.
より大きな配列の確保には malloc を用いるべき.
*/
/* 和 */
void add(double v3[], double v1[], double v2[], int n)
{
int i;
for(i=0; i<n; i++)
v3[i] = v1[i] + v2[i];
/* 呼出側の配列の値が変更されることに注意. */
/* C言語では配列を返す関数がないので, */
/* このように呼出側で配列を用意してその内容を変更する. */
}
/* 差 */
void subtract(double v3[], double v1[], double v2[], int n)
{
int i;
for(i=0; i<n; i++)
v3[i] = v1[i] - v2[i];
}
/* 内積 */
double product(double v1[], double v2[], int n)
{
int i;
double x = 0.0;
for(i=0; i<n; i++)
x+= v1[i]*v2[i];
return x;
}
/* ベクトルの内容を表示. */
void print_vector(double v[], int n)
{
int i;
for(i=0; i<n; i++)
printf("v[%d]=%g\n", i, v[i]);
}
int main(void)
{
int i;
int dimension = 5;
double x;
double v1[dimension]; // 可変長配列の初期化は宣言時には行えない.
double v2[dimension];
double v3[dimension];
for(i=0; i<dimension; i++){
v1[i] = (double)i;
v2[i] = (double)i+10.0;
v3[i] = 0.0;
}
add(v3, v1, v1, dimension);
subtract(v3, v1, v2, dimension);
x = product(v1, v2, dimension);
print_vector(v3, dimension);
printf("x=%g\n", x);
return EXIT_SUCCESS;
}
#include <stdio.h>
#include <stdlib.h>
/*
行列をベクトルに演算.
行列X行列みなすことにすると, n次元のベクトルv[n]は nX1次元の行列m[m][1]
として 扱えばよい.
*/
/* C90:
大きさを引数として与えて表示するためにはポインターが必要.
C99:
void print_matrix33(int n, double m[n][n]) のように大きさを引数として
与えることができる. 前から順に評価されるので, 大きさを先に与えること.
引数の引数の並び順を変えて, void print_matrix33(double m[n][n], int n) の
ようにすると煩雑なのでやらない方がいい.
*/
void print_matrix33(double m[3][3])
{
int i, j;
for(i=0; i<3; i++){
for(j=0; j<3; j++)
printf("%g\t", m[i][j]);
printf("\n");
}
printf("\n");
}
void print_matrix31(double m[3][1])
{
int i, j;
for(i=0; i<3; i++){
for(j=0; j<1; j++)
printf("%g\t", m[i][j]);
printf("\n");
}
printf("\n");
}
int main(void)
{
int i, j, k;
double m33[3][3] = {{1.0, 2.0, 3.0},
{4.0, 5.0, 6.0},
{7.0, 8.0, 9.0}};
double v1[3][1] = {{1.0},
{2.0},
{3.0}};
double v2[3][1] = {{0.0},
{0.0},
{0.0}};
/* 行列をベクトルに演算 */
for(i=0; i<3; i++)
for(j=0; j<1; j++)
for(k=0; k<3; k++)
v2[i][j] += m33[i][k] * v1[k][j];
print_matrix33(m33);
print_matrix31(v1);
print_matrix31(v2);
return EXIT_SUCCESS;
}
#include <stdio.h>
#include <stdlib.h>
/*
行列をベクトルに演算.
ベクトルを1次元配列で表した.
keyword: ベクトル, 配列, 行列, 積
*/
void print_matrix33(double m[3][3])
{
int i, j;
for(i=0; i<3; i++){
for(j=0; j<3; j++)
printf("%g\t", m[i][j]);
printf("\n");
}
printf("\n");
}
void print_vector3(double v[3])
{
int i;
for(i=0; i<3; i++)
printf("%g\n", v[i]);
printf("\n");
}
int main(void)
{
int i, j;
double m33[3][3] = {{1.0, 2.0, 3.0},
{4.0, 5.0, 6.0},
{7.0, 8.0, 9.0}};
double v1[3] = {1.0, 2.0, 3.0};
double v2[3] = {0.0, 0.0, 0.0};
/* 行列をベクトルに演算 */
for(i=0; i<3; i++)
for(j=0; j<3; j++)
v2[i] += m33[i][j] * v1[j];
print_matrix33(m33);
print_vector3(v1);
print_vector3(v2);
return EXIT_SUCCESS;
}
#include <stdio.h>
#include <stdlib.h>
/*
行列の積を求める.
行列 A, B, C の要素をそれぞれ a_{ij}, b_{ij}, c_{ij}とするとき,
行列の積 C = A B は要素で表現すると
c_{ij} = Σ_{k=1}^{n} a_{ik} b_{kj}
であることに注意.
*/
void print_matrix23(double m[2][3])
{
int i, j;
for(i=0; i<2; i++){
for(j=0; j<3; j++)
printf("%g\t", m[i][j]);
printf("\n");
}
printf("\n");
}
void print_matrix34(double m[3][4])
{
int i, j;
for(i=0; i<3; i++){
for(j=0; j<4; j++)
printf("%g\t", m[i][j]);
printf("\n");
}
printf("\n");
}
void print_matrix24(double m[2][4])
{
int i, j;
for(i=0; i<2; i++){
for(j=0; j<4; j++)
printf("%g\t", m[i][j]);
printf("\n");
}
printf("\n");
}
int main(void)
{
int i, j, k;
double m23[2][3] = {{1.0, 2.0, 3.0},
{4.0, 5.0, 6.0}};
double m34[3][4] = {{1.0, 2.0, 3.0, 4.0},
{5.0, 6.0, 7.0, 8.0},
{9.0, 10.0, 11.0, 12.0}};
double m24[2][4] = {{0.0}, {0.0}};
/* 行列の積 */
for(i=0; i<2; i++)
for(j=0; j<4; j++)
for(k=0; k<3; k++)
m24[i][j] += m23[i][k] * m34[k][j];
print_matrix23(m23);
print_matrix34(m34);
print_matrix24(m24);
return EXIT_SUCCESS;
}
#include <stdio.h>
#include <stdlib.h>
/*
行列の積を求める.
行列 A, B, C の要素をそれぞれ a_{ij}, b_{ij}, c_{ij}とするとき,
行列の積 C = A B は要素で表現すると
c_{ij} = Σ_{k=1}^{n} a_{ik} b_{kj}
であることに注意.
*/
void print_matrix(int m, int n, double x[m][n])
{
int i, j;
for(i=0; i<m; i++){
for(j=0; j<n; j++)
printf("%g\t", x[i][j]);
printf("\n");
}
printf("\n");
}
int main(void)
{
int i, j, k;
double m23[2][3] = {{1.0, 2.0, 3.0},
{4.0, 5.0, 6.0}};
double m34[3][4] = {{1.0, 2.0, 3.0, 4.0},
{5.0, 6.0, 7.0, 8.0},
{9.0, 10.0, 11.0, 12.0}};
double m24[2][4] = {{0.0}, {0.0}};
/* 行列の積 */
for(i=0; i<2; i++)
for(j=0; j<4; j++)
for(k=0; k<3; k++)
m24[i][j] += m23[i][k] * m34[k][j];
print_matrix(2, 3, m23);
print_matrix(3, 4, m34);
print_matrix(2, 4, m24);
return EXIT_SUCCESS;
}
#include <stdio.h>
#include <stdlib.h>
/*
行列の積を求める.
C99の可変長配列を用いた.
行列の要素を出力する関数に加え, 積を求める関数を作成した.
keyword: C99, 2次元配列
行列 A, B, C の要素をそれぞれ a_{ij}, b_{ij}, c_{ij}とするとき,
行列の積 C = A B は要素で表現すると
c_{ij} = Σ_{k=1}^{n} a_{ik} b_{kj}
であることに注意.
*/
void print_matrix(int m, int n, double x[m][n])
{
int i, j;
for(i=0; i<m; i++){
for(j=0; j<n; j++)
printf("%g\t", x[i][j]);
printf("\n");
}
printf("\n");
}
void multiply(int L, int M, int N,
double x[L][M], double a[L][N], double b[N][M])
{
int i, j, k;
for(i=0; i<L; i++)
for(j=0; j<M; j++)
for(k=0; k<N; k++)
x[i][j] += a[i][k] * b[k][j];
}
int main(void)
{
double m23[2][3] = {{1.0, 2.0, 3.0},
{4.0, 5.0, 6.0}};
double m34[3][4] = {{1.0, 2.0, 3.0, 4.0},
{5.0, 6.0, 7.0, 8.0},
{9.0, 10.0, 11.0, 12.0}};
double m24[2][4] = {{0.0}, {0.0}};
multiply(2, 4, 3, m24, m23, m34);
print_matrix(2, 3, m23);
print_matrix(3, 4, m34);
print_matrix(2, 4, m24);
return EXIT_SUCCESS;
}
struct vector {
struct vector *this;
struct dimension;
double (*set_heitht)(void);
double (*set_width)(void);
double (*get_heitht)(void);
double (*get_width)(void);
double (*get_area)(void);
};
(c)1999-2013 Tetsuya Makimura